Integer Partitions

MA 367 Spring 2003

Richard Hitt

•The Number of Integer Partitions

Mathematica has built-in functions for counting the number of partitions of an integer.  PartitionsP counts the total number of partitions of an integer, while PartitionsQ counts the number of partitions that use distinct summands.

In[1]:=

PartitionsP[10]

Out[1]=

42

In[2]:=

PartitionsQ[10]

Out[2]=

10

The asymptotic behaviour of these functions can be studied numerically

In[3]:=

g1 = ListPlot[Table[{n, Log[PartitionsP[n]]}, {n, 1, 100}]]

[Graphics:HTMLFiles/partitions_6.gif]

Out[3]=

-Graphics -

In[4]:=

g2 = ListPlot[Table[{n, Log[PartitionsQ[n]]}, {n, 1, 100}]]

[Graphics:HTMLFiles/partitions_9.gif]

Out[4]=

-Graphics -

In[5]:=

Show[g1, g2]

[Graphics:HTMLFiles/partitions_12.gif]

Out[5]=

-Graphics -

Since the natural log of the number of partitions grows like a square root curve, this suggest that the P[n] is of order e^(n/2).

•Enumerating Partitions

The Combinatorica add-in package has functions that aid in enumerating and other calculations.

In[6]:=

<< DiscreteMath`Combinatorica`

In[7]:=

Partitions[10]

Out[7]=

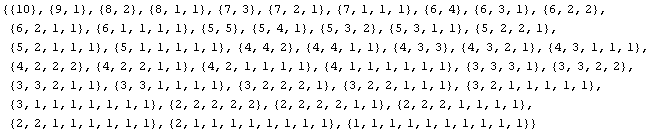
{{10}, {9, 1}, {8, 2}, {8, 1, 1}, {7, 3}, {7, 2, 1}, {7, 1, 1, 1}, {6, 4}, {6, 3, 1}, {6, 2, 2 ... , 1, 1, 1}, {2, 2, 1, 1, 1, 1, 1, 1}, {2, 1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}

In[8]:=

Partitions[10] // Length

Out[8]=

42

There is also a function for drawing Ferrers diagrams.

In[9]:=

FerrersDiagram[RandomPartition[100]]

[Graphics:HTMLFiles/partitions_21.gif]

Out[9]=

-Graphics -

The Combinatorica add-in also has the ability to enumerate partitions of an integer using summands that don't exceed a given number.

In[10]:=

Partitions[10, 3]

Out[10]=

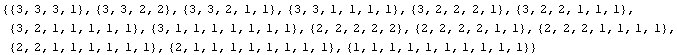
{{3, 3, 3, 1}, {3, 3, 2, 2}, {3, 3, 2, 1, 1}, {3, 3, 1, 1, 1, 1}, {3, 2, 2, 2, 1}, {3, 2, 2, 1 ... , 1, 1, 1}, {2, 2, 1, 1, 1, 1, 1, 1}, {2, 1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}

We can make a table of these.

In[11]:=

Table[Partitions[m, n] // Length, {m, 1, 10}, {n, 1, 10}] // MatrixForm

Out[11]//MatrixForm=

( 1 1 1 1 1 1 1 1 1 1 ) 1 2 2 2 2 2 2 2 ... 1 5 12 18 23 26 28 29 30 30 1 6 14 23 30 35 38 40 41 42

In order to construct a method for counting the number of partitions of an integer m into exactly n parts, we can use the above function.  Then we can build a table of values for the number of partitions of m using exactly n parts that illustrates the recurrence that we talked about in class.  Of course, this method is very inefficient since it uses the Mathematica functions that actually enumerate the partitions (only counting the total number of such) rather that constructing the numbers using a more efficient recurrence relation.

In[12]:=

Clear[a] ; a[m_, n_] := 1 /; n == 1 a[m_, n_] := Length[Partitions[m, n]] - Length[Partitions[m, n - 1]] /; n > 1

In[15]:=

Table[a[m, n], {m, 1, 25}, {n, 1, 25}] // MatrixForm

Out[15]//MatrixForm=

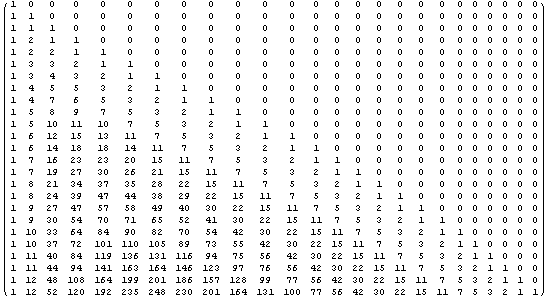
( 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ... 201 164 131 100 77 56 42 30 22 15 11 7 5 3 2 1 1

•Implementing the Recurrence Relation

The above method for generating the table of values is very inefficient since it actually enumerates the partitions and simply counts the number of such.  Since we have a recurrence relation given by

p (m, n) = Underoverscript[∑, i = 1, arg3] p (m - n, i)

we can directly implement this in Mathematica.

In[22]:=

p[m_, n_] := 1 /; n == 1 ; p[m_, n_] := 1 /; m == n ; p[m_, n_] := 0 /; n > m ; p[m_, n_] := Sum[p[m - n, i], {i, 1, n}] ;

We can now define a new function for calculating a table of the partition numbers p(m,n) that runs more efficiently than what we did before.

In[26]:=

PartitionTable[a_, b_] := TableForm[ Table[p[m, n], {m, 1, a}, {n, 1, b}], TableSpacing -> {1, 1}, TableHeadings -> Automatic ]

Now we can use the PartitionTable function to compute tables of a partition numbers much more quickly.

In[29]:=

PartitionTable[25, 25]

Out[29]//TableForm=
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 1 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 1 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
6 1 3 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
7 1 3 4 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
8 1 4 5 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
9 1 4 7 6 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 1 5 8 9 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
11 1 5 10 11 10 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 1 6 12 15 13 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
13 1 6 14 18 18 14 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0
14 1 7 16 23 23 20 15 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0
15 1 7 19 27 30 26 21 15 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0 0
16 1 8 21 34 37 35 28 22 15 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0 0
17 1 8 24 39 47 44 38 29 22 15 11 7 5 3 2 1 1 0 0 0 0 0 0 0 0
18 1 9 27 47 57 58 49 40 30 22 15 11 7 5 3 2 1 1 0 0 0 0 0 0 0
19 1 9 30 54 70 71 65 52 41 30 22 15 11 7 5 3 2 1 1 0 0 0 0 0 0
20 1 10 33 64 84 90 82 70 54 42 30 22 15 11 7 5 3 2 1 1 0 0 0 0 0
21 1 10 37 72 101 110 105 89 73 55 42 30 22 15 11 7 5 3 2 1 1 0 0 0 0
22 1 11 40 84 119 136 131 116 94 75 56 42 30 22 15 11 7 5 3 2 1 1 0 0 0
23 1 11 44 94 141 163 164 146 123 97 76 56 42 30 22 15 11 7 5 3 2 1 1 0 0
24 1 12 48 108 164 199 201 186 157 128 99 77 56 42 30 22 15 11 7 5 3 2 1 1 0
25 1 12 52 120 192 235 248 230 201 164 131 100 77 56 42 30 22 15 11 7 5 3 2 1 1

Converted by Mathematica  (February 20, 2003)