The Pendulum

Ma 507

November 8, 2000

Richard Hitt

Introduction

Consult section 7.4 in the Greenberg's text for details..

Getting started

Every Maple worksheet should begin by re-initializing the Maple "kernel" and loading the additional packages that we are most likely to use.

> restart;

> with( plots ):

> with( DEtools ):

Warning, the name changecoords has been redefined

The Undamped Pendulum

We begin with the undamped pendulum.

> DE1 := diff(theta(t),t,t) + g/L*sin(theta(t)) = 0;

> LDE1 := diff(theta(t),t,t) + g/L*theta(t) = 0;

Now for a specific example, let's suppose we have a 1 kg mass on a 1 meter pendulum.

> g:=9.8:L:=1:

We plot the solution to DE1 in blue and to LDE1 in red using an initial condition in which the mass is released from rest after a deflection of 1 radian from the equilibrium position.

> Plot1 := DEplot(DE1,theta(t),t=0..10,[[theta(0)=1,D(theta)(0)=1]],stepsize=.1,linecolor=blue):

> Plot2 := DEplot(LDE1,theta(t),t=0..10,[[theta(0)=1,D(theta)(0)=1]],stepsize=.1,linecolor=red):

> display(Plot1,Plot2);

Exercise 1: Explain what the graphs show. Does the period of the solution to the linearized pendulum correspond to what you expected? In other words: you can compute the exact period of the linearized pendulum; do so; does the computer period correspond the what you see on the graph?

Next we look at the phase plane graphs of ' versus . First we do the linearized case.

> IC :=[[0,3,0],[0,2.5,0],[0,2,0],[0,1.5,0],[0,1,0],[0,.5,0]];

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+9.8*theta(t)=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, arrows=none, linecolor=blue
);

Exercise 2: According to exercise #8, these orbits are ellipses. Verify this mathematically.

Another way to see the orbits is to graph 3-space curves given by ( ) and then just look straight down the t-axis.

> DEplot3d(
{diff(theta(t),t)=v(t),diff(v(t),t)+9.8*theta(t)=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, orientation=[0,90], linecolor=blue);

Exercise 3: In the above graph, left-click the mouse in the graph and drag the graph around while holding down the mouse button. Explain what you see.

Next we look at the orbits in the ' state space for the nonlinear pendulum.

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+9.8*sin(theta(t))=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, arrows=none, linecolor=blue
);

Exercise 4: Explain what you see in the above graphs.

In the linearized pendulum, the period is independent of the initial conditions. Discuss what happens to the period in the nonlinear pendulum as the initial conditions vary.

All the above examples used an initial velocity of 0. If we allow the initial velocity to vary, then we can get orbits that never close up in the state space.

> InitCond := [seq([0,0,i],i=1..10)];

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+9.8*sin(theta(t))=0},
[theta(t),v(t)], t=0..2, InitCond, stepsize=.05, arrows=none, linecolor=blue);

Exercise 5: Explain the above graphs.

The Damped Pendulum

> DE1 := diff(theta(t),t,t) + c/m*diff(theta(t),t) + g/L*sin(theta(t)) = 0;

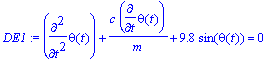
> LDE1 := diff(theta(t),t,t) + c/m*diff(theta(t),t) + g/L*theta(t) = 0;

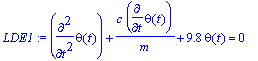
> g:=9.8:L:=1:m:=1:c:=.1:

> Plot1 := DEplot(DE1,theta(t),t=0..10,[[theta(0)=1,D(theta)(0)=1]],stepsize=.1,linecolor=blue):

> Plot2 := DEplot(LDE1,theta(t),t=0..10,[[theta(0)=1,D(theta)(0)=1]],stepsize=.1,linecolor=red):

>

> display(Plot1,Plot2);

>

Next we look at the phase plane graphs of ' versus . First we do the linearized case.

> IC :=[[0,3,0],[0,2.5,0],[0,2,0],[0,1.5,0],[0,1,0],[0,.5,0]];

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+0.1*v(t)+9.8*theta(t)=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, arrows=none, linecolor=blue
);

Note that these orbits are not ellipses as in the undamped case. They do not close up.

Another way to see the orbits is to graph 3-space curves given by ( ) and then just look straight down the t-axis.

> DEplot3d(
{diff(theta(t),t)=v(t),diff(v(t),t)+0.1*v(t)+9.8*theta(t)=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, orientation=[0,90], linecolor=blue);

Exercise 6: In the above graph, left-click the mouse in the graph and drag the graph around while holding down the mouse button. Explain what you see.

Next we look at the orbits in the ' state space for the nonlinear pendulum.

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+0.1*v(t)+9.8*sin(theta(t))=0},
[theta(t),v(t)], t=0..2, IC, stepsize=.05, arrows=none, linecolor=blue
);

Exercise 7: Explain what you see in the above graphs.

In the linearized pendulum, the period is independent of the initial conditions. Discuss what happens to the period in the nonlinear pendulum as the initial conditions vary.

All the above examples used an initial velocity of 0. If we allow the initial velocity to vary, then we can get orbits that never close up in the state space.

> InitCond := [seq([0,0,6+i/4],i=1..8)];

> DEplot(
{diff(theta(t),t)=v(t),diff(v(t),t)+0.2*v(t)+9.8*sin(theta(t))=0},
[theta(t),v(t)], t=0..6, InitCond, stepsize=.05, arrows=none, linecolor=blue);

>

Exercise 8: Explain the above graphs.